Problem-Solving Strategy for AC Steady-State Analysis
STEP 1. For relatively simple circuits (e.g., those with a single source), use
- Ohm’s law for ac analysis—that is, $\mathbf V = \mathbf I\mathbf Z$
- The rules for combining $\mathbf Z_s$ and $\mathbf Y_p$
- KCL and KVL
- Current and voltage division
STEP 2. For more complicated circuits with multiple sources, use
- Nodal analysis
- Loop analysis
- Superposition
- Source transformation
- Thévenin’s and Norton’s theorems
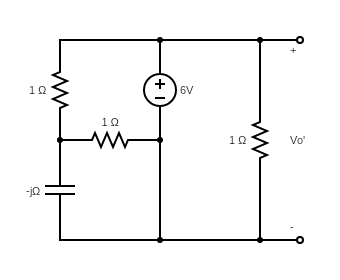
PROBLEM:
Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed.
If there are any errors in solution, please let me know in the comments
SOLUTION:
$\mathbf V_o'=6V$
$\frac{\mathbf V_1}{-j}-4+\frac{\mathbf V_1}{2}=0$
$\mathbf V_1=\frac{4}{j+0.5}=(1.6-3.2j)V$
So, $\mathbf V_o''=\frac{\mathbf V_1}{2}=(0.8-1.6j)V$
Then, $\mathbf V_o=\mathbf V_o'+\mathbf V_o''=6+0.8-1.6j=6.9857\angle-13.2405\,^{\circ}V$
Related Posts: Superposition


Comments
Post a Comment