Superposition

Problem-Solving Strategy for applying the superposition

STEP 1. In a network containing multiple independent sources, each source can be applied independently with the remaining sources turned off.

STEP 2. To turn off a voltage source, replace it with a short circuit, and to turn off a current

source, replace it with an open circuit.

STEP 3. When the individual sources are applied to the circuit, all the circuit laws and techniques we have learned, or will soon learn, can be applied to obtain a solution.

STEP 4. The results obtained by applying each source independently are then added together algebraically to obtain a solution.

PROBLEM:

Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed. 

If there are any errors in solution, please let me know in the comments

SOLUTION:

$3k \Omega$ and $6k \Omega$ are connected in parallel. Their combined resistance is

$3k \Omega || 6k \Omega=\frac{3k \times 6k}{3k+6k} =2k \Omega$

$I_{o1}$ can then be calculated as

$I_{o1}=\frac{12}{2k+2k+4k}=1.5mA$

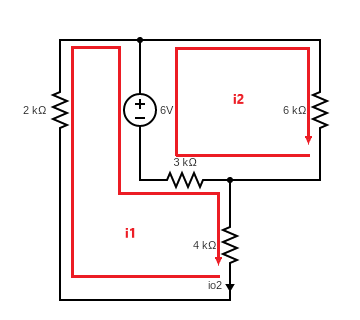
Using loop analysis, we can find $I_{o2}$

$2kI_1+6+3k(I_1-I_2)+4kI_1=0$

$6kI_2+3k(I_2-I_1)-6=0$

Combining these equations yields

$I_1=I_{o2}=-0.5mA$

Using loop analysis, we can find $I_{o3}$

$2kI_3+3k(I_3-I_4)+4kI_3=0$

$6kI_4-12+3k(I_4-I_3)=0$

Combining these equations yields

$I_3=I_{o3}=0.5mA$

$3k \Omega$ and $6k \Omega$ are connected in parallel. Their combined resistance is

$3k \Omega || 6k \Omega=\frac{3k \times 6k}{3k+6k} =2k \Omega$

$I_{o4}$ can then be calculated as

$I_{o4}=-2mA \times\frac{2k}{2k+6k}=-0.5mA$

Therefore, $I_o$ is

$I_o=I_{o1}+I_{o2}+I_{o3}+I_{o4}=1mA$

Related Posts: Simplifying Resistor Combination(EASY PROBLEM)

                   Series and Parallel Resistor Combination(MORE DIFFICULT)

                   Loop Analysis Technique