Problem-Solving Strategy for AC Steady-State Analysis
STEP 1. For relatively simple circuits (e.g., those with a single source), use
- Ohm’s law for ac analysis—that is, $\mathbf V = \mathbf I\mathbf Z$
- The rules for combining $\mathbf Z_s$ and $\mathbf Y_p$
- KCL and KVL
- Current and voltage division
STEP 2. For more complicated circuits with multiple sources, use
- Nodal analysis
- Loop analysis
- Superposition
- Source transformation
- Thévenin’s and Norton’s theorems
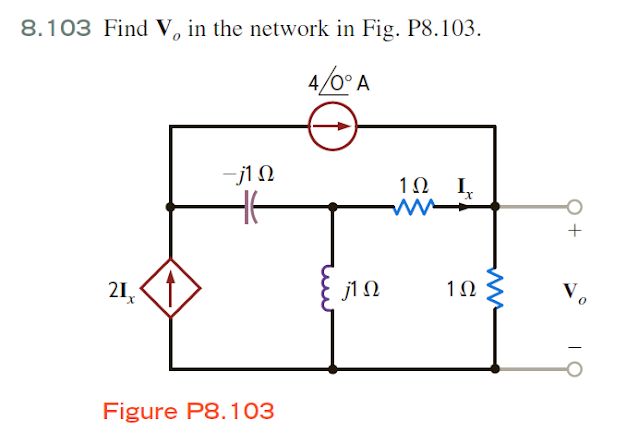
PROBLEM:
Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed.
If there are any errors in solution, please let me know in the comments
SOLUTION:
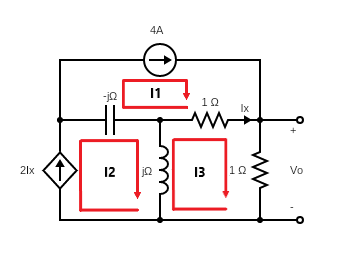
The loop equations are
$\mathbf I_1=4A$
$\mathbf I_2=2\mathbf I_x$
$j(\mathbf I_3-\mathbf I_2)+1(\mathbf I_3-\mathbf I_1)+\mathbf I_3=0$
$\mathbf I_x=\mathbf I_3-\mathbf I_1$
Combining these equations,
$\mathbf I_3=\frac{4-8j}{2-j}=3.2-2.4j=4\angle-36.87\,^{\circ}A$
Therefore, $\mathbf V_o=1\times \mathbf I_3=4\angle-36.87\,^{\circ}V$
Related post: Loop Analysis Technique
Comments
Post a Comment