Maximum Average Power Transfer

Problem-Solving Strategy for solving the Maximum Average Power Transfer

STEP 1. Remove the load $\mathbf Z_L$ and find the Thevenin equivalent for the remainder of the circuit.

STEP 2. Construct the Thevenin equivalent circuit with the load $\mathbf Z_L$.

STEP 3. Select $\mathbf Z_L=\mathbf Z^{*}_{Th}=R_{Th}-jX_{Th}$, and then $\mathbf I_L=\frac{\mathbf V_{Th}}{2R_{Th}}$ and the maximum average power transfer$=\frac{1}{2}\mathbf I^2_LR_{Th}=\frac{\mathbf V_{Th}^2}{8R_{Th}}$.

PROBLEM:

Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed.

If there are any errors in solution, please let me know in the comments

SOLUTION:

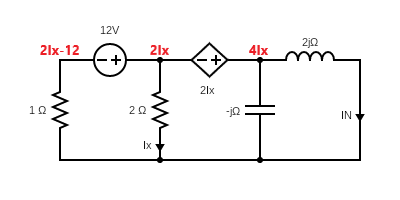
In the figure above, we can apply KCL to find $\mathbf I_x$ first.

$\frac{2\mathbf I_x-12}{1}+\mathbf I_x+\frac{4\mathbf I_x}{-j}=0$

$\mathbf I_x=(1.44-1.92j)A$

So

 $\mathbf V_{Th}=4\mathbf I_x=(5.76-7.68j)V$

We can also apply KCL to find $\mathbf I_x$ and $\mathbf I_N$

$\frac{2\mathbf I_x-12}{1}+\mathbf I_x+\frac{4\mathbf I_x}{-j}+\frac{4\mathbf I_x}{2j}=0$

$\mathbf I_x=(2.769-1.846j)A$

Therefore

$\mathbf I_{N}=\frac{4\mathbf I_x}{2j}=(-3.692-5.538j)A$

The Thevenin equivalent impedance is then

$\mathbf Z_{Th}=\frac{\mathbf V_{Th}}{\mathbf I_N}=(0.48+1.36j)\Omega$

Thus, the load impedance should be

$\mathbf Z_L=(0.48-1.36j)\Omega$

Hence, the maximum average power transferred to the load is

$P_L=\frac{1}{2}\mathbf I^2_LR_{Th}=\frac{\mathbf V_{Th}^2}{8R_{Th}}=24W$

Related posts: Instantaneous Power

                   RMS Value

                   Complex Power