Series and Parallel Resistor Combinations(MORE DIFFICULT)

Problem-Solving Strategy for solving the Series and Parallel Resistor Combinations

STEP 1. If Resistors $R_1$ and $R_2$ are in series, their combined resistor $R_S=R_1+R_2$

STEP 2. If Resistors $R_1$ and $R_2$ are in parallel, their combined resistor $R_P=\frac{R_1R_2}{R_1+R_2}$

Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed.

If there are any errors in solution, please let me know in the comments

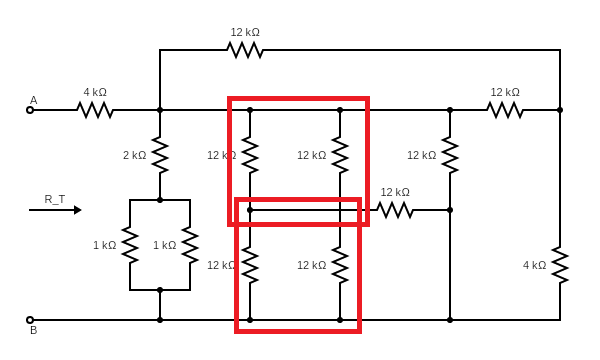
The two $12k \Omega$ can be removed as they are shorted.

The two $12k \Omega$ are connected in parallel. Their combined resistance is

$12k \Omega || 12k \Omega=\frac{12k \times 12k}{12k+12k} =6k \Omega$

$12k \Omega$ and $6k \Omega$ are connected in parallel. Their combined resistance is

$12k \Omega || 6k \Omega=\frac{12k \times 6k}{12k+6k} =4k \Omega$

The two $12k \Omega$ are connected in parallel. Their combined resistance is

$12k \Omega || 12k \Omega=\frac{12k \times 12k}{12k+12k} =6k \Omega$

$12k \Omega$ and $6k \Omega$ are connected in parallel. Their combined resistance is

$12k \Omega || 6k \Omega=\frac{12k \times 6k}{12k+6k} =4k \Omega$

The two $1k \Omega$ are connected in parallel. Their combined resistance is

$1k \Omega || 1k \Omega=\frac{1k \times 1k}{1k+1k} = 0.5k \Omega$

And $2k \Omega$ and $0.5k \Omega$ are connected in series. Their combined resistance is

$2k \Omega + 0.5k \Omega = 2.5k \Omega$

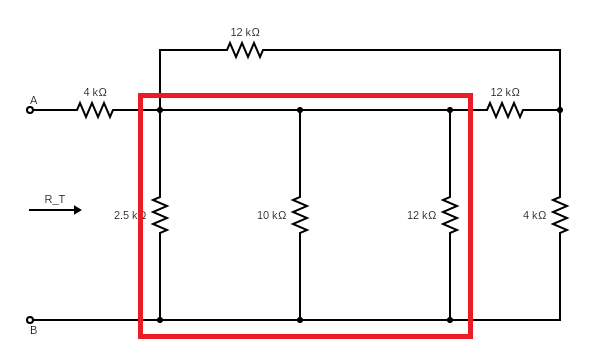
$6k \Omega$ and $4k \Omega$ are connected in series. Their combined resistance is

$6k \Omega + 4k \Omega = 10k \Omega$

$2.5k \Omega$ , $10k \Omega$ and $12k \Omega$ are connected in parallel. Their combined resistance is

$2.5k \Omega || 10k \Omega || 12k \Omega=\frac{1}{\frac{1}{2.5k}+\frac{1}{10k}+\frac{1}{12k}} =1.714k \Omega$

The two $12k \Omega$ are connected in parallel. Their combined resistance is

$12k \Omega || 12k \Omega=\frac{12k \times 12k}{12k+12k} =6k \Omega$

$6k \Omega$ and $4k \Omega$ are connected in series. Their combined resistance is

$6k \Omega + 4k \Omega = 10k \Omega$

$1.714k \Omega$ and $10k \Omega$ are connected in parallel. Their combined resistance is

$1.714k \Omega || 10k \Omega=\frac{1.714k \times 10k}{1.714k+10k} =1.463k \Omega$

$4k \Omega$ and $1.463k \Omega$ are connected in series. Their combined resistance is

$4k \Omega + 1.463k \Omega = 5.463k \Omega$

Therefore, $R_T$ is

$R_{T}=5.463k \Omega$