Source Transformation

Problem-Solving Strategy for applying the Source Transformation

STEP 1. A voltage source $v$ in series with a resistor $R$ can be replaced with a current source of value$ i =\frac{v}{R}$ in parallel with the resistor $R$. (From Thevenin equivalent circuit to Norton equivalent circuit)

STEP 2. A current source of $i$ in parallel with the resistor $R$ can be replaced with a a voltage source of value $v=iR$ in series with a resistor $R$. (From Norton equivalent circuit to Thevenin equivalent circuit)

PROBLEM:

Note: This post is based on Irwin's Basic Engineering Circuit Analysis 11th ed. 

If there are any errors in solution, please let me know in the comments

SOLUTION:

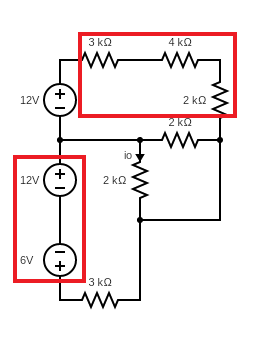
In the figure above, the circuit not marked in red are short-circuited. So we can get:

$6k \Omega$ and $3k \Omega$ are connected in parallel. Their combined resistance is

$6k \Omega || 3k \Omega=\frac{6k \times 3k}{6k+3k} =2k \Omega$

Now we can convert the current source and resistor into the voltage source and same resistor.

Since $12V$ source and $-6V$ source are connected in series, we can get $6V$ source. Also, $3k \Omega$, $4k\Omega$ and $2k \Omega$ are connected in series. Their combined resistance is

$3k \Omega+4k \Omega+2k \Omega=9k \Omega$

In this case, we can change the voltage source and resistor into the current source and same resistor

Since $2mA$ source and $-\frac{4}{3}mA$ source are connected in parallel, we can get $\frac{2}{3}mA$ source. Also, $3k \Omega$, $2k\Omega$ and $9k \Omega$ are connected in parallel. Their combined resistance is

$3k \Omega || 2k \Omega || 9k \Omega=\frac{1}{\frac{1}{3k}+\frac{1}{2k}+\frac{1}{9k}} =\frac{18}{17}k \Omega$

Therefore, $I_o=\frac{2}{3} \times \frac{\frac{18}{17}k}{\frac{18}{17}k+2k}=\frac{3}{13}mA$

Related Posts: Thevenin's Theorem

                   Norton's Theorem